Existence of high horizontal stresses in rock masses
At any depth z in rock of specific weight y the vertical stress,
σv = yz
Since the rock mass at the ground surface is unrestrained in the vertical direction and free to expand upwards, there do not appear to be any other factors, in addition to the weight, capable of significantly affecting the magnitude of the vertical principal stress (where the ground surface is horizontal). However, this is not the case in horizontal directions, where in addition to effects due to the weight of the rock, the mode of formation of the rock and its subsequent history may be of great importance.
The earliest attempt on the problem of defining the state of stress of a rock mass appears to be by Albert Heim, who in 1878 directed attention to the probability of the hydrostatic state of stress at depth. In this state the rock is in compression, equal in all directions (there is no shear ing stress), and equal to the weight of a column of rock of unit area above the point considered. He considered that the strength of a rock type could be expressed as the maximum possible height of a column of rock. In a higher column the weight of the rock itself would crush the lower part of the column. Thus at a depth greater than the critical column height, plasticity of the rock would develop, leading, in time, to an equalization of the principal stresses. Heim’s hydrostatic hypothesis has been much discussed and criti cized (for instance by Talobre(2) and by Ouliaoff(3) but in the absence of actual measurements the hydrostatic state of stress has often been assumed.
For relatively shallow depths below the earth's surface, another hypothesis has been developed based on the theory of elasticity. In rock with Poisson's ratio μ, which has been laterally confined during its formation :
N = μ/1−μ (Refs, l and 4).
For many rocks it is between 0.2 and 0.25 and hence N lies between ¼ and ⅓.
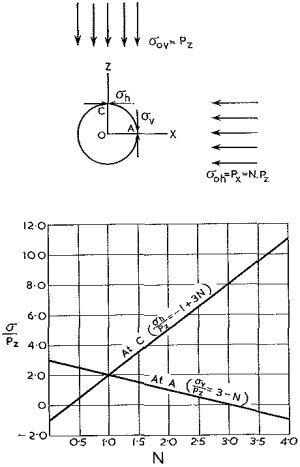
Fig. 1,—Relation between the Circumferential Principal Stress at the Surface of a Circular Tunnel and the Ratio N. (Terzaghi and Richart1.)
